MKKC Package

Overview

The MKKC package performs the robust multiple kernel k-means clustering using min-max optimization. The method is proposed by Bang, Yu, and Wu (2019). The main function-mkkc performs a robust clustering on multi-view data collected from different sources. This package also includes 18 multi-view simulation data generated for illustration purpose. We will give a short tutorial on using MKKC on the simulation data and assess how robustly it performs when noise and redundancy are present in the multi-view data.

Installation

Users can install the package from github as follows:

install.packages("devtools")
library(devtools)
devtools::install_github("SeojinBang/MKKC")

Usage

mkkc performs the multiple kernel K-means clustering on multi-view data. The usage is

mkkc(K, centers, iter.max, epsilon)

where

K is N × N × P array containing P kernel matrices with size N × N.
centers is the number of clusters, say k.
iter.max is the maximum number of iterations allowed. The default is 10.
epsilon is a onvergence threshold. The default is 10⁻⁴.

One can perform the clustering analysis using the most basic call to mkkc:

mkkc(K, centers)

The function mkkc returns an object of class MultipleKernelKmeans which has print and coef method. The output includes a vector of clustering labels to which each point is allocated ($cluster) and kernel coefficients ($coefficients). See the documentation page of mkkc for detail:

??mkkc
help(mkkc, package = "MKKC")

Simulation Data

The object multiviews contains multi-view simulation data used in Bang et. al (2018), which aims to access how robustly mkkc performs a clustering when noise or redundant information are present in multi-view data. The simulation data sets are composed of multiple views generated from three clusters with 100 samples for each the cluster. The data sets also include the true label which is a factor-type vector with three levels (100 cases for each).

See the documentation page of multiviews for details:

??multiviews
help(multiviews, package = "MKKC")

Example

In this tutorial, we will describe how to use mkkc to cluster multi-view data using a simulation data set created beforehand. In particular, we will examine how robustly mkkc concatenates multiple views when noise is present in the multi-view data. Users can either use their own data or use any of the simulated data saved in the workplace.

We first load the MKKC package:

library(MKKC)

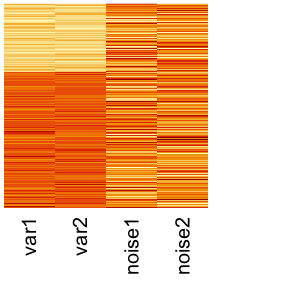
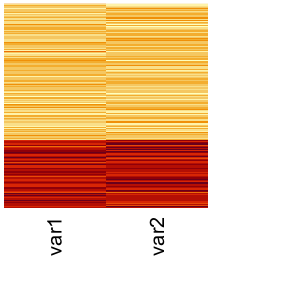
In this example, we use a simulation data set simBnoise which is composed of two partial views. Each partial view only conveys partial information so that each view alone cannot completely detect the three clusters. The first view (View 1) is able to detect the first cluster but not able to identify the difference between the second and third cluster. The second view (View 2) is able to detect the third cluster but cannot identify the difference between the first and second cluster. Additionally, View 1 has 10 noise variables that have no information about the clusters, while we will use only 2 noise variables added to View 1.

truelabel <- simBnoise$true.label
n.noise <- 2                                    # number of noises to be added
dat1 <- simBnoise$view1[,c(1:(2 + n.noise))]    # view 1
dat2 <- simBnoise$view2                         # view 2

We can visualize the multi-view data using heatmap:

heatmap(dat1, scale = "column", Rowv = NA, Colv = NA, labRow = NA, cexCol = 1.5)    # view 1
heatmap(dat2, scale = "column", Rowv = NA, Colv = NA, labRow = NA, cexCol = 1.5)    # view 2

Construct Kernel Matrices

The function mkkc takes a kernel matrix for each view as an input. In this tutorial, we use a RBF kernel for all the views, while users can use any view-specific kernel functions. We use a package kernlab to define the RBF kernel and calculate kernel matrice from the views.

require(kernlab)

rbf <- rbfdot(sigma = 0.5)        # define a RBF kernel
dat1 <- kernelMatrix(rbf, dat1)   # kernel matrix from View 1
dat2 <- kernelMatrix(rbf, dat2)   # kernel matrix from View 2

Construct Multi-view Data

Centering and scaling of kernel matrices in multi-view learning allow multiple views comparable with each other. Hence, we recommand to standardize the kernel matrices before combining them. Each kernel matrix is centered by K ← K – J_nK – K J_n + J_nK J_n and scaled by K ← nK/tr(K) where J_n = 1_n1_n^T/n and n is the number of samples.

We standardize the kernel matrices using a function StandardizeKernel provided by MKKC. With the standarized kernel matrices, we construct a multi-view data as a 300 × 300 × 2 array.

n.view = 2    # the number of views used
K = array(NA, dim = c(nrow(dat1), ncol(dat1), n.view))
K[,,1] = StandardizeKernel(dat1, center = TRUE, scale = TRUE)
K[,,2] = StandardizeKernel(dat2, center = TRUE, scale = TRUE)

Multiple Kernel k-Means Clustering

We perform the clustering using the most basic call to mkkc. It requires a multi-view data set K and the number of clusters centers. We run the clustering using the multi-view simulation data constructed above and set centers = 3.

res <- mkkc(K = K, centers = 3)

## iter  1 ... theta  0.5 0.5 
## iter  2 ... theta  0.9554583 0.295126 
## iter  3 ... theta  0.9059099 0.4234705 
## iter  4 ... theta  0.9140981 0.405493 
## iter  5 ... theta  0.913377 0.4071147 
## iter  6 ... theta  0.913442 0.4069689 
## iter  7 ... theta  0.9134362 0.406982

res is an object of class MultipleKernelKmeans which has a print and a coef method. We can obtain a vector of clustering labels by res$cluster and kernel coefficients of the two views by coef(res).

A comprehensive summary of the clustering is displayed with use of the print function:

print(res)

## 
## Multiple kernel K-means clustering with 3 clusters of sizes  103, 97, 100 
## 
## Kernel coefficients of views:
## [1] 0.9134362 0.4069820
## 
## Clustering vector:
##   [1] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
##  [36] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
##  [71] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 1 2 2 2 2
## [106] 2 2 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
## [141] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
## [176] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1
## [211] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
## [246] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
## [281] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
## 
## Within cluster sum of squares by cluster:
##  cluster1  cluster2  cluster3 
## 0.3285893 0.2897978 0.3103318 
## (between_SS / total_SS =   29.7  %)
## 
## Within cluster sum of squares by cluster for each view:
##        cluster1  cluster2  cluster3
## view1 0.3045793 0.2710080 0.2882098
## view2 0.1237784 0.1038114 0.1156576
## 
## Available components:
##  [1] "cluster"         "totss"           "withinss"       
##  [4] "withinsscluster" "withinssview"    "tot.withinss"   
##  [7] "betweenssview"   "tot.betweenss"   "clustercount"   
## [10] "coefficients"    "size"            "iter"           
## [13] "H"               "call"

It displays kernel coefficients, clustering vector (clustering label assigned to the samples), within cluster sum of squares by cluster, and within cluster sum of squares by cluster for each view.

License

The MKKC package is licensed under the GPL-3 (http://www.gnu.org/licenses/gpl.html).

References

Bang, Seojin, Yaoliang Yu, and Wei Wu. 2019. “Robust Multiple Kernel K-Means Clustering Using Min-Max Optimization.” ArXiv Preprint ArXiv:1803.02458.

MKKC

Robust Multiple Kernel K-means Clustering Using Min-Max Optimization